Binäre Bäume

Binäre Bäume

Zweifach verkettete Listen , Bäume

Ähnlich wie die zuvor definierten einfach verketteten Listen lassen sich auch komplexere Strukturen mit Hilfe von Zeigern

definieren. Will man etwa eine FIFO-Struktur mit Hilfe von Zeigern aufbauen, dann ist eine einfach verkettete Liste nicht

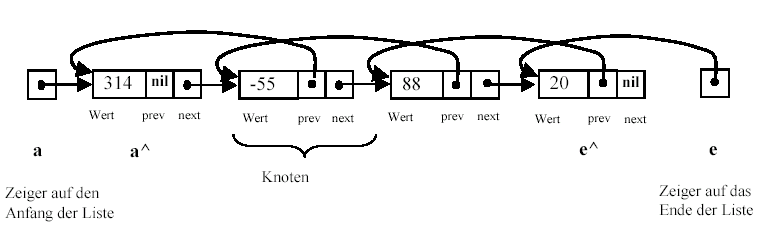
geeignet, da man dort nur von einem Ende unmittelbar auf die Listenelemente zugreifen kann. Hier bietet sich eine doppelt

verkettete Liste an, die unten schematisch dargestellt ist.

Bäume

Häufig sollen Daten hierarchisch gespeichert werden. Dies bedeutet, dass ein Datensatz "Oberelement" von mehreren "Unterelementen" ist; man spricht auch von Vater und Kindern. Diese können wiederum Väter von mehreren Unterelementen sein usw. Weil die Struktur immer weiter verästelt, wird sie auch Baum genannt:

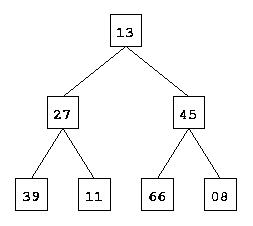
Das oberste Element (die Elemente in Bäumen heißen übrigens Knoten, weil Bäume Graphen sind) ist die Wurzel, die Elemente in der untersten Reihe stellen die Blätter dar. Der abgebildete Baum zeichnet sich außerdem dadurch aus, dass jeder Knoten genau zwei Nachfolger hat - es handelt sich um einen binären Baum.

Man kann sich den Baum ähnlich wie eine verkettete Liste vorstellen, nur daß jedes Element nicht nur einen, sondern mehrere Nachfolger hat. Ist die Anzahl der Nachfolger fest, ist daher die Implementation recht einfach, wie z. B. im Falle eines binären Baums für Zahlen:



type
   PBinTree = ^TBinTree;
   TBinTree = record
                 Num    : Integer;
                 Links  : PBinTree;
                 Rechts : PBinTree;
              end;

(Die Namen Links und Rechts sind natürlich beliebig, genauso gut könnten sie Up und Down oder Charme und Strange heißen.) Auch, bzw. gerade Bäume sind natürlich rekursive Datenstrukturen; um Bäume zu durchsuchen, sind rekursive Algorithmen häufig die naheliegendste Lösung. Wie erwähnt, werden Bäume normalerweise eingesetzt, um Daten hierarchisch zu speichern. Ein bekanntes Beispiel sind hierarchische Dateisysteme - unter Windows NT bspw. kann man sich mit dem Befehl tree die Verzeichnisse als Baum anzeigen lassen. Unter Unix-Systemen zeigt pstree die Prozeßhierarchie an.

Die Graphen werden, wegen ihrer Ähnlichkeit mit Bäumen auch Bäume genannt, wobei die Wurzel des Baumes dann oben liegt. Bäume sind geordnete Bäume, wenn jeder Knoten aus geordneten Verzweigungen besteht. Ein Knoten y, der direkt 'unter' einem Knoten x liegt, heißt direkter Nachfolger von x. x ist dann direkter Vorgänger von y. Ein Baum wird in Stufen eingeteilt. Die Wurzel liegt auf Stufe 1. Die größte Stufe heißt seine Tiefe oder Höhe. Elemente ohne Nachfolger heißen Blätter, alle anderen Elemente heißen innere Knoten.

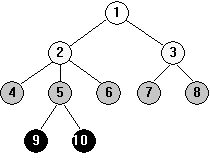
Der Grad eines Knotens ist die Anzahl seiner Nachfolger. Der höchste Grad eines Knotens ist der Grad des Baumes. Die Weglänge eines Knotens ist die Anzahl der Verbindungen, die von der Wurzel bis zu diesem Knoten zu durchlaufen sind. Die Wurzel hat die Weglänge 1, ihre direkten Nachfolger 2, usw. Von besonderer Bedeutung sind geordnete Bäume vom Grad 2. Sie heißen binäre Bäume. Beim nicht leeren binären Baum besteht jeder Knoten aus einem linken und einem rechten binärem Teilbaum. Ein Beispiel für binäre Bäume (einfach Bäume genannt) sind arithmetische Ausdrücke:

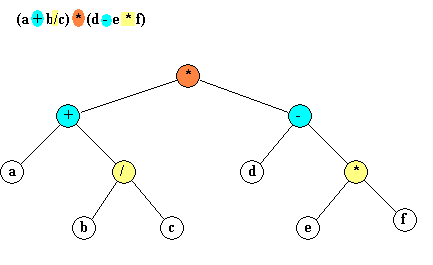
Binäre Baume sind vollständig ausgeglichen, wenn sich für jeden Knoten die Zahl der Knoten in seinem linken und rechten Teilbaum um höchstens eins unterscheiden.

Durchsuchen eines Baumes und Einfügen in einen Baum

Eine typische Aufgabe ist das Suchen nach einem bestimmten Schlüssel in einem Baum, bzw.. bei nicht Vorhandensein das Einfügen dieses Schlüssels. Nachfolgend ein Pascalprogramm für diese Aufgabenstellung, wobei mitgezählt wird, wie oft ein Schlüssel vorkommt.

PROGRAM baum_suchen;
USES crt;

TYPE richtung  = ^node;
     node      = RECORD
                       schluessel         : integer;
                       counter            : integer;
                       links, rechts      : richtung;
            END;

VAR k       : integer;
    wurzel  : richtung;

PROCEDURE suchen (x : integer; VAR p : richtung);

BEGIN
  IF p = nil THEN  BEGIN          { x nicht vorhanden }
    new (p);         
    WITH p^ DO BEGIN
      schluessel  := x;           { x einfuegen }
      counter     := 1;
      links       := nil;
      rechts      := nil;
    END;
  END
  ELSE
    IF x < p^.schluessel THEN
      suchen (x, p^.links)        { im linken Teilbaum weitersuchen }
    ELSE
      IF x > p^.schluessel THEN
        suchen (x, p^.rechts)     { im rechten Teilbaum weitersuchen }
      ELSE
        p^.counter := p^.counter + 1; { counter hochzaehlen }
 END {suchen};

PROCEDURE anzeigen (w : richtung; l : integer);
  VAR i : integer;

BEGIN
  IF w<>nil THEN
    WITH w^ DO BEGIN
      anzeigen (links, l+1);
      FOR i := 1 TO l DO
        WRITE ('   ');
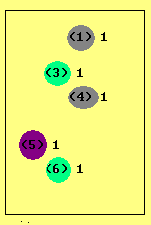
      WRITELN ('(', schluessel, ')' , ' ' ,counter);{Schluessel-Anzahl }
      anzeigen (rechts, l+1);
    END;
END{anzeigen};

{++++++++++++++Hauptprogramm++++++++++++++}

BEGIN
     clrscr;
     wurzel := nil;
     READ (k);                    { Schluessel k lesen }
          WHILE k<>0 DO
            BEGIN
              suchen (k, wurzel); { k suchen bzw. einfuegen }
              READ (k);           { naechsten Schluessel lesen }
            END;
     anzeigen(wurzel,0);          { Baum zeigen }
     READLN;
END.